DFS for finding strongly connected components

SCC(G):
	Input: directed graph G = (V,E) in adjacency list
	Output: labeling of V by strongly connected component
		1. Construct G^R
		2. Run DFS on G^R
		3. Order V by decreasing post order number.
		4. Run directed DFS on G using the vertex ordering from before and
		   label the connected components we reach.

Additional property

In addition to labelling the connected components the order we have labelled them is in reverse topological ordering. This is because we always start at the next sink vertex after we have labelled a component.

This takes as we do two runs of a DFS algorithm.

Correctness Proof

Find this in Week 6 - Graph algorithms - strongly connected components.

Example

Suppose we want to find the strongly connected components of the graph below.

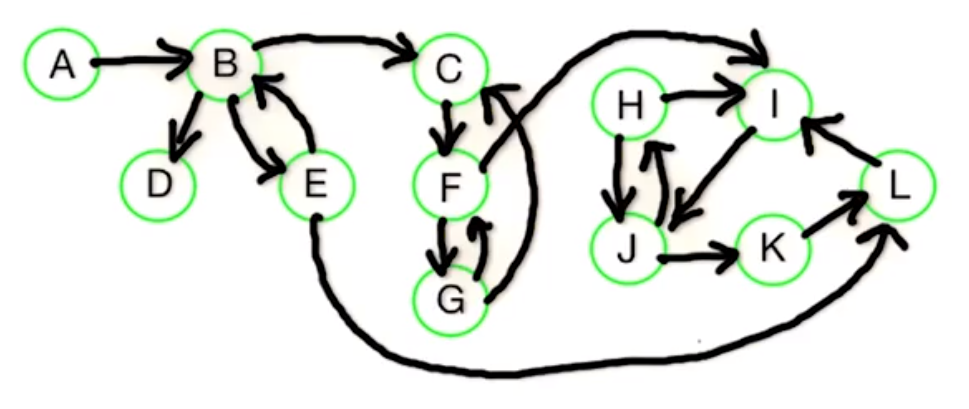
First we look at and run the DFS to find path in an undirected graph algorithm.

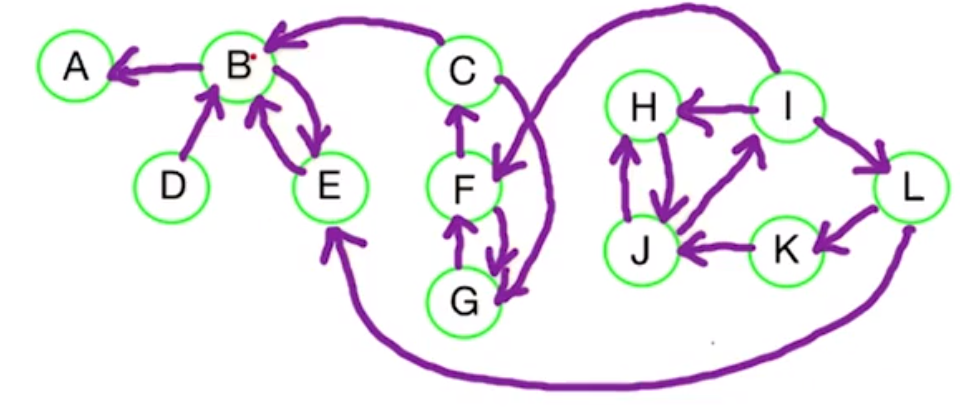
This gives us - in this example we started at and did a fairly random vertex ordering.

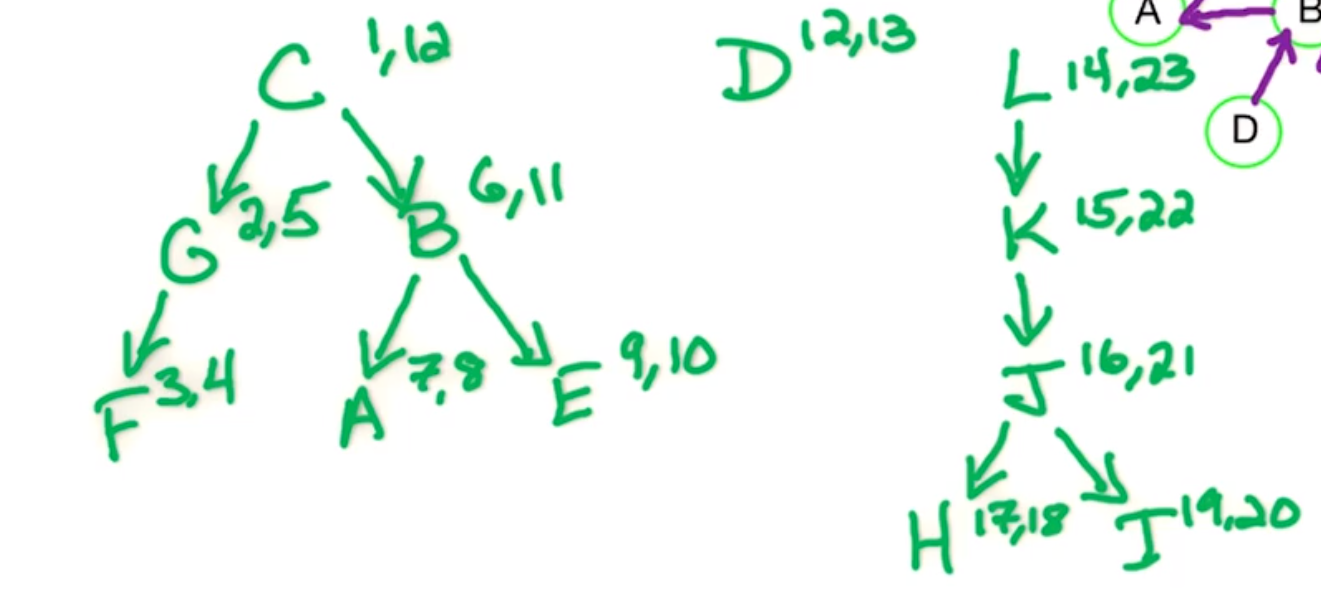
Letter	Pre	Post
A	7	8
B	6	11
C	1	12
D	12	13
E	9	10
F	3	4
G	2	5
H	17	18
I	19	20
J	16	21
K	15	22
L	14	23

Then we order the vertices by reverse post order.

Letter	L	K	J	I	H	D	C	B	E	A	G	F
Post	23	22	21	20	18	13	12	11	10	8	5	4

Now run a connected components DFS using the vertex ordering above.

Letter	L	K	J	I	H	D	C	B	E	A	G	F
Post	23	22	21	20	18	13	12	11	10	8	5	4
CC	1	1	1	1	1	2	3	4	4	5	3	3

Notice also that the strongly connected component graph is the following.

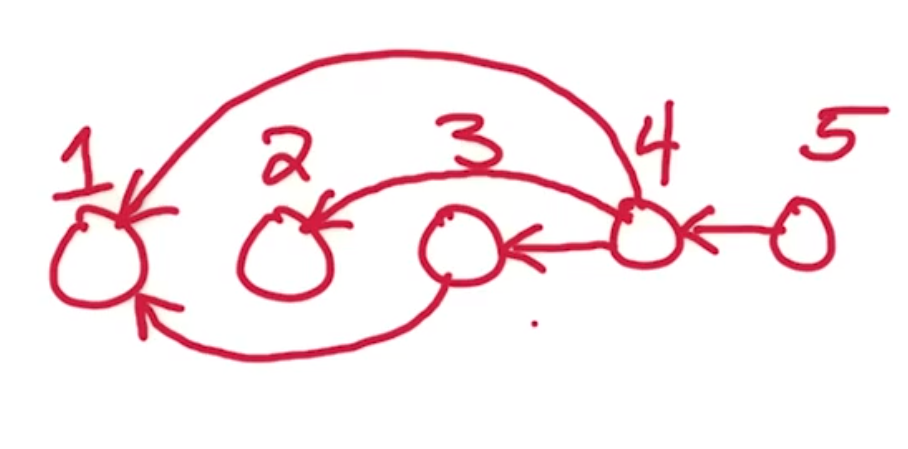
Giving that our ordering is exactly a reverse topological sorting.