Week 10 - NP overview

Complexity classes

Nondeterministic Polynomial time (NP)

Nondeterministic Polynomial time (NP)

This definition can mean multiple things.

Nondeterministic Polynomial time (search)

The class of NP problems is the class of all search problems.

Otherwise it might mean.

Nondeterministic Polynomial time (decision)

The class of NP problems is the class of all decision problems.

Link to original

In this class we use the search problem definition.

Search problems

Search problem

A problem is a search problem if we can verify a solution in polynomial time.

Formally:

The problem is of the form, for a given instance of the problem you can either:

• find a solution for if one exists, or
• output no if has no solutions.

Then this problem is a search problem if given an instance and a solution then we can verify that is a solution to in polynomial time in .

Link to original

Note here we have.

Statement

Lemma

The class of Polynomial time problems is a subset of Nondeterministic Polynomial time (NP).

Link to original

There is an open problem.

P equals NP or P not equals NP

This is the open problem whether the class of Polynomial time problems is equal to the class of Nondeterministic Polynomial time (NP) problems.

Link to original

Satisfiability

Statement

Sat Problem

Given a boolean function in CNF with variables and clauses. Is there a true/false assignment to the variables that satisfies . If yes then output it, otherwise say no.

Link to original

The Satisfiability problem is in NP

Statement

Lemma

The Satisfiability problem is in NP.

Proof

First note that it is in the form of a search problem as it either provides you with a satisfying assignment to the variables or says one doesn’t exist.

All that is left to show is that we can verify an answer in Polynomial time.

Given an assignment of values to the -variables. To check one clause is satisfied takes time. There are clauses, so this in total takes time.

This is polynomial so the Satisfiability problem is in NP.

Link to original

k-colourings problem

Statement

-colourings problem (graphs)

Given an undirected graph and integer . Does have a proper vertex colouring using -colours, if it does output the colouring and if not say so.

Link to original

The k-colourings problem is in NP

Statement

Lemma

The k-colourings problem (graphs) is in NP.

Proof

The problem is of the correct from for a search problem as you either have to provide a proper vertex k-colouring or you have to say no such colouring exists.

If you are given and a -colouring it takes time to check the colouring is proper by checking every edges vertices.

Link to original

MST

Statement

Minimum Spanning Tree problem

Given an undirected graph with weights can you find a spanning tree with minimum weight

Link to original

Minimum Spanning Tree problem is in NP

Statement

Lemma

Minimum Spanning Tree problem (MST) is in NP

Proof

The problem is in the correct form for a search problem. It outputs a MST always as one always exists from the definition.

To verify a solution as we can first check it is a spanning tree by running BFS to verify it is connected and checking the size of the edge set is to check it is a tree. To check it is minimal we can find a solution in polynomial time using Kruskal’s algorithm. We can just check it’s weight vs the weight of the proposed solution to check they match.

Link to original

This proof was relatively easy as MST is a polynomial time problem. This is shown by what is above and Kruskal’s algorithm.

Knapsack problem

Statement

The knapsack problem

Given objects with weight and value how do we maximise the value of a bag that can carry weight . The solution to this is a subset of objects such that:

• , and
• it maximises its value .

Link to original

Whilst the Knapsack problem is of the correct form to be a search problem we can’t currently check if a solution is correct in polynomial time. Therefore the Knapsack problem isn’t known to be in NP.

Similarly we say that the Knapsack problem isn’t known to be in polynomial time either.

We say it isn’t known to be as there might be a super clever algorithm that happens to solve the Knapsack problem in polynomial time.

However, there is a variant of the problem that is in NP.

Statement

Knapsack-search (without replacement)

Given objects with weight and value , and a goal is there a bag that has weight less than but value at least . The solution to this is a subset of objects such that:

• , and
• .

If there is such a bag what is it otherwise say there is no such solution.

Link to original

Here instead of having to check if a solution is maximal we can instead just check if it has enough value.

Knapsack-search is NP

Statement

Lemma

Knapsack-search is in NP.

Proof

The problem statement is in the form of a search problem.

Given a proposed solution to check if it solves the problem we just need to calculate and check the following.

This takes time, so is polynomial.

This makes Knapsack-search run in polynomial time.

Link to original

Polynomial time and Nondeterministic Polynomial time

Note that NP isn’t Not Polynomial time. In fact we have the following result.

Polynomial time is a subset of NP-complete

Statement

Lemma

The class of Polynomial time problems is a subset of Nondeterministic Polynomial time (NP).

Proof

If the problem is in NP then we already know the problem is a search problem. Therefore it is in the class Nondeterministic Polynomial time.

Link to original

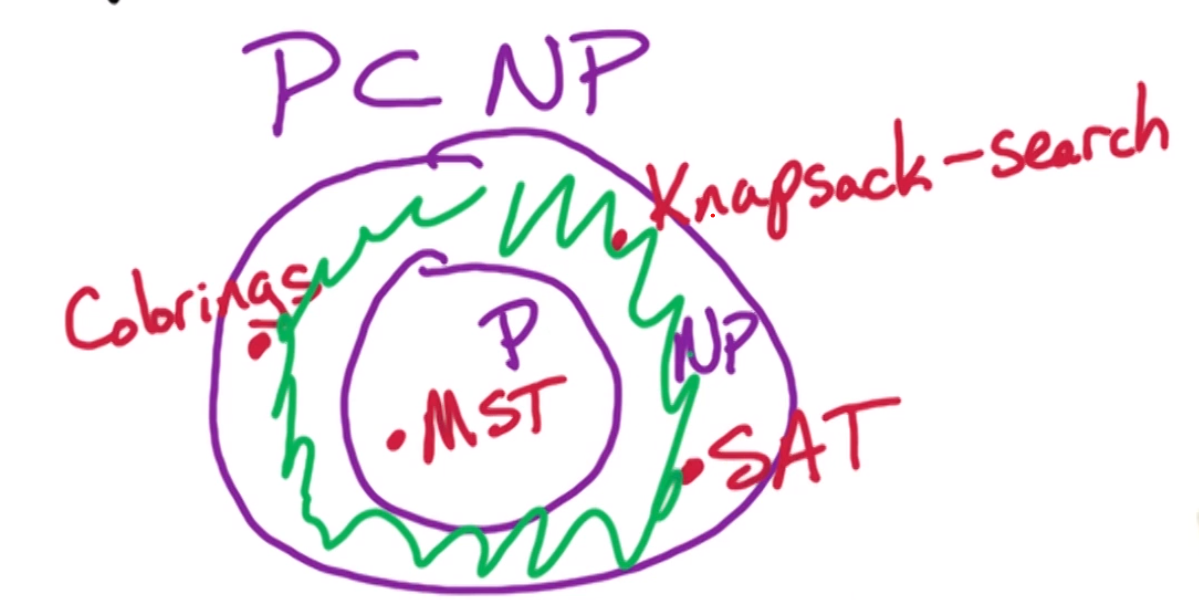
The question is, are there problems that are in NP but are not in P?

NP-complete

If P not equal to NP then we would have a problem in NP that didn’t lie in P. Therefore the green region above would be non-empty.

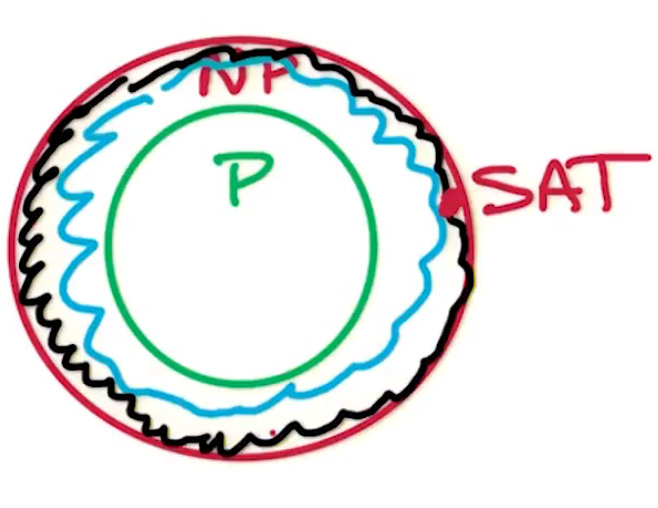
Therefore lets look at the hardest problems in NP.

NP-hard

NP-hard

A problem is NP-hard if for all search problems there is a many-one reduction from to . In other terms, is as hard as any search problem.

Link to original

We define a many-one reduction as bellow.

Many-one reduction (problem)

Many-one reduction

There is a many-one reduction of problem to ( or ) if a polynomial time algorithm to solve would also solve in polynomial time.

Link to original

However, we want to look at the hardest problems in NP.

NP-Complete

NP-Complete

A problem is NP-complete if

• is NP, and
• is NP-hard.

Link to original

A classic NP-Complete problem is the SAT problem.

Reductions functionally

To show a many-one reduction from to you need to construct a way to transform an instance of problem into some input to the problem . This needs to be done in polynomial time. Then the solution from solving in problem should relate back to the solution of problem . Either you should construct a way to transform the solution from problem into a solution to problem or forward on the fact that no solution can exist.

Transclude of reduction

Therefore to show reduces to we need:

• Define : Show how an instance of problem can be converted into an instance of problem in polynomial time.
• Define : Show how a solution to the problem can be converted into a solution to problem in polynomial time.
• Proof: Show that a solution for exists if and only if a solution to exists.

Showing NP-Complete

To show a problem is NP-Complete need to show

• is in NP, and
• is NP-hard.

Generically showing is NP-hard, is ironically quite hard. However we get around this by having some NP-complete problems already, such as the SAT problem. Then to show is NP-hard we just need to show another NP-Complete problem reduces to it. So functionally we show:

• is NP, and
• there is some NP-complete problem that reduces to .

Practice problems

From Algorithms by S. Dasgupta, C. Papadimitriou, and U. Vazirani.

8.1 Optimisation vs Search problems

8.2 Search problems vs Decision problems