DFS to find path in a directed graph

Finding paths in a directed graph via DFS

To do this we are going to use a DFS algorithm like but we are going to track pre/postorder numbers.

DFS(G)
  input: G = (V,E) in adjacency list representation
  output: Vertices labelled by connected components
    clock = 1
    for all v in V, set visited(v) = False
    for all v in V
      if not visited(v) then
        explore(v)
  return post (defined in Explore)

Explore(z)
  input: vertex z
    pre(z) = clock, clock ++
    visited(z) = True
    for all (z, w) in E
      if not visited(w)
        Explore(w)
	post(z) = clock, clock++

Example

Suppose we have the following graph and let be the root node. Suppose we explore edges alphabetically and lets run the algorithm above on it.

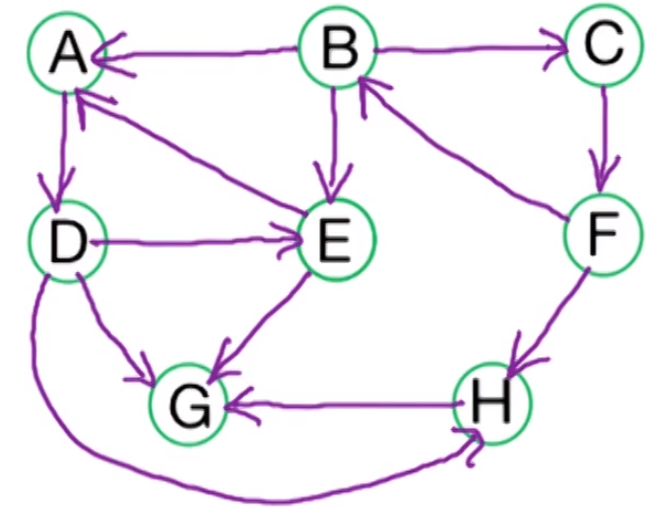
As we are using DFS we explore far first and then slowly come back. Which gives us the following DFS tree with the pre/post numbers.

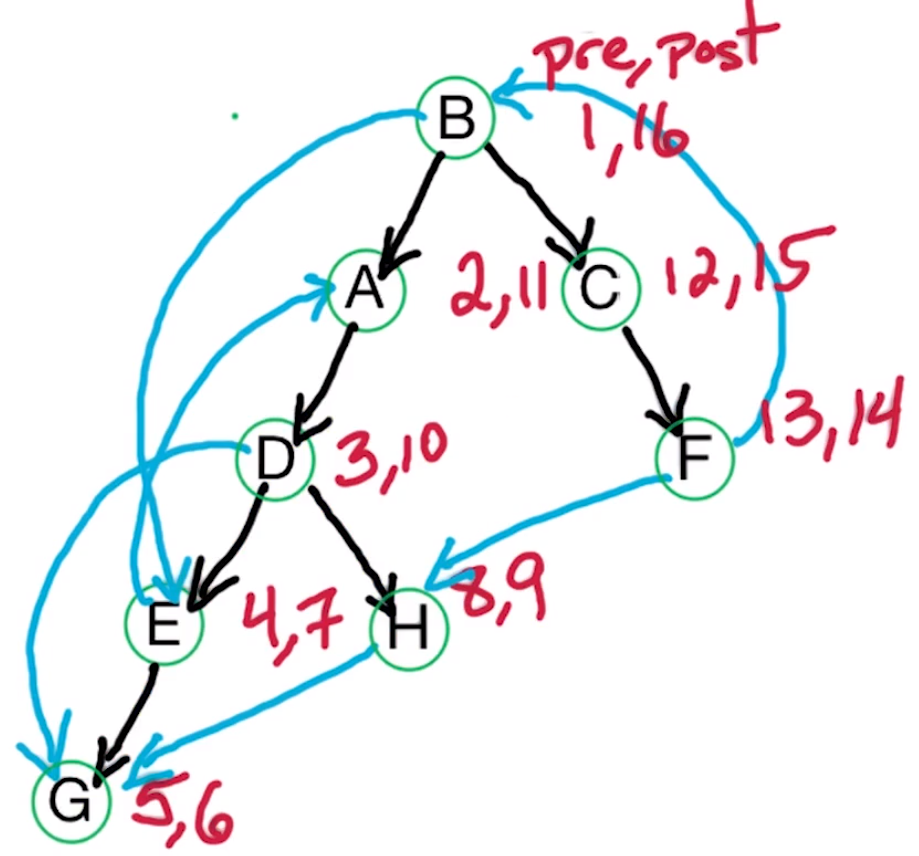
Letter	Pre	Post
A	2	11
B	1	16
C	12	15
D	3	10
E	4	7
F	13	15
G	5	6
H	8	9