Week 3 - Linear-Time Median

Median list problem

Given an unsorted list of numbers - you want to find the median () element.

Not usual Median definition

This isn’t the usual definition of median, which in the case of odd would return the mean of the and elements.

Though we can solve a more generic problem.

th smallest element

Given an unsorted list of numbers - you want to find the ‘th smallest element.

Using Merge sort

A basic algorithm would be to use Merge sort on then output the -th element of that list which would take . Though is it possible to do this without sorting ?

Using divide and conquer better

Quick sort

We are going to use ideas from quick sort algorithm.

The basic idea is summed up in following pseudocode

Select(A, k):
1. Choose a piviot p.
2. Partition A into A_{<p}, A_{=p}, and A_{>p}.
3. If k <= |A_{<p}| then return Select(A_{<p}, k)
4. If |A_{<p}| < k <= |A_{<p}| + |A_{=p}| then retrun p.
5. Otherwise return Select(A_{>p}, k - (|A_{<p}| + |A_{=p}|))

Though we have skipped how we choose a pivot. We need that pivot is close to the median to get a good running time. Lets assume the running time of this algorithm is for input of size .

Choosing the pivot

We say a pivot is good if We want to find such a in time. This will give us which by Masters theorem gives .

Random pivot

If I choose any random element then it has It takes time to check if is good and if we kept randomly drawing elements we have Therefore this algorithm has expected runtime of - though this is not worst case run time.

Recursive pivot

Instead of finding a median of we could instead aim for a median of a “representative sample”.

Trick

Divide into sets of 5 and find the median of each of these sets. Call this set . Then find the median of the set .

Let be the sets of size and (assume is a multiple of ). Then the median of each have 2 elements less than and 2 elements greater than . Therefore the median of has less than or equal to it and elements greater or equal to it.

Which gives and . This gives that is a good pivot from the definition.

FastSelect(A,k):
1. Break A into ceiling of n/5 groups, G_i with atmost 5 elements in.
2. For i = 1 -> n/5 sort G_i and let m_i = median(G_i)
3. Let S = {m_1, ..., m_{n/5}}
4. Let p = FastSelect(S,n/10)
5. Partition A into A_{<p}, A_{=p}, A_{>p}.
6. Return based on the following conditions.
	1. If k <= |A_{<p}| then return FastSelect(A_{<p}, k)
	2. If k > |A_{<p}| + |A_{=p}| then return
	   FastSelect(A_{>p}, k - |A_{<p}| + |A_{=p}|)
	3. Else return p.

Breaking into groups requires one sweep through so that takes us time.

Sorting a single takes where is the constant runtime of your favourite sorting algorithm on 5 elements.

We run this sort on elements giving step 2 takes time.

We then run our algorithm on a subproblem of size having run time .

Pivot runtime

So finding this pivot takes time.

Partitioning the set takes time.

The last step of the algorithm takes at most from the assumption about the good pivot.

Combining this all together we have As we have that .

Why is this true?

I don’t know, but this looks like it could be solved using Akra–Bazzi method or Recursion tree method.

Useful discussion about this

Let me see if I can help explain this. I find the best way to solve recurrences with multiple sub-problems is to think in terms of the “recursive tree”.

For the recurrence what do we know? We know there is work at each level, and that we generate two recursive calls, each with a shrinking portion of . At the first level of recursion we have two sub-problems, one of size , and a second of size ​, so the total work at that level is . What about the second level down? Let’s visualize it:

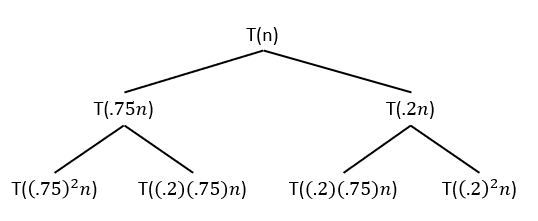
And the work at this second level? Sum up the four leaves, and you get: So the amount of work at each level is shrinking! This tells us that the work at the top level, O(n), dominates.

Now, what happens with the recurrence ? Draw the tree, do the math:

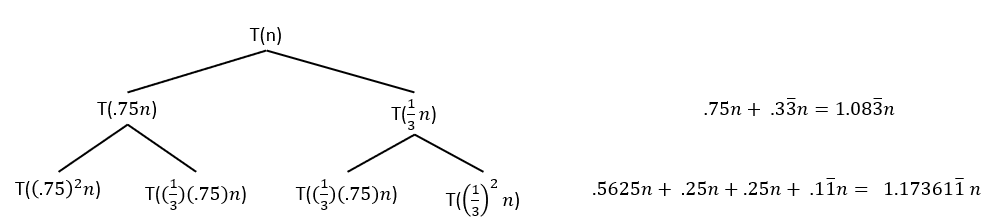
Now we see that at each level the work increases, so we no longer have a linear overall run time. The work at the bottom of the recursive stack will dominate the overall runtime.

What’s the intuition behind this? The overall number of operations at each level is bounded by the total n at that level. As you make successive recursive calls, does n shrink? does it grow? or is it held constant?

Further questions

Change 5 in the analysis

What happens to the run time if we switch out 5 for 3 or 7 in the analysis of this algorithm?

If we use instead of the run time is the same. If we use instead of 5 we get